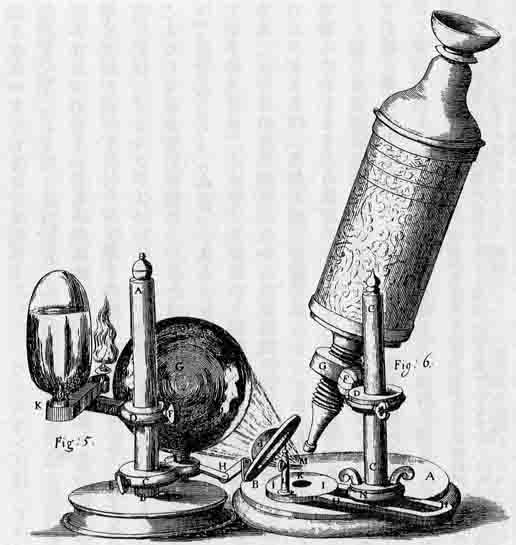
右図がレーベンフックが愛用した鍛レンズ顕微鏡です。一方、当時すでに多くの複式顕微鏡が作られており、ロバート・フックも複式顕微鏡を使用していました(下図)。当時のレンズは、あまり良質ではなかったので、2枚のレンズを使った顕微鏡では、レンズの歪み(レンズ収差)が非常に大きくなり、解像度を上げることはできませんでした。ロバート・フックの塩湯していた顕微鏡は、その倍率がせいぜい50倍程度だったようです。レーベンフックは、むしろ1枚のレンズを使った顕微鏡の方が解像度が高く、200倍程度まで拡大して観察できることに注目しました。レーベンフックは、室の高いレンズの製作にも力を注ぎました。
シングルレンズ顕微鏡

ロバート・フックの複式顕微鏡
シングルレンズ顕微鏡のしくみ
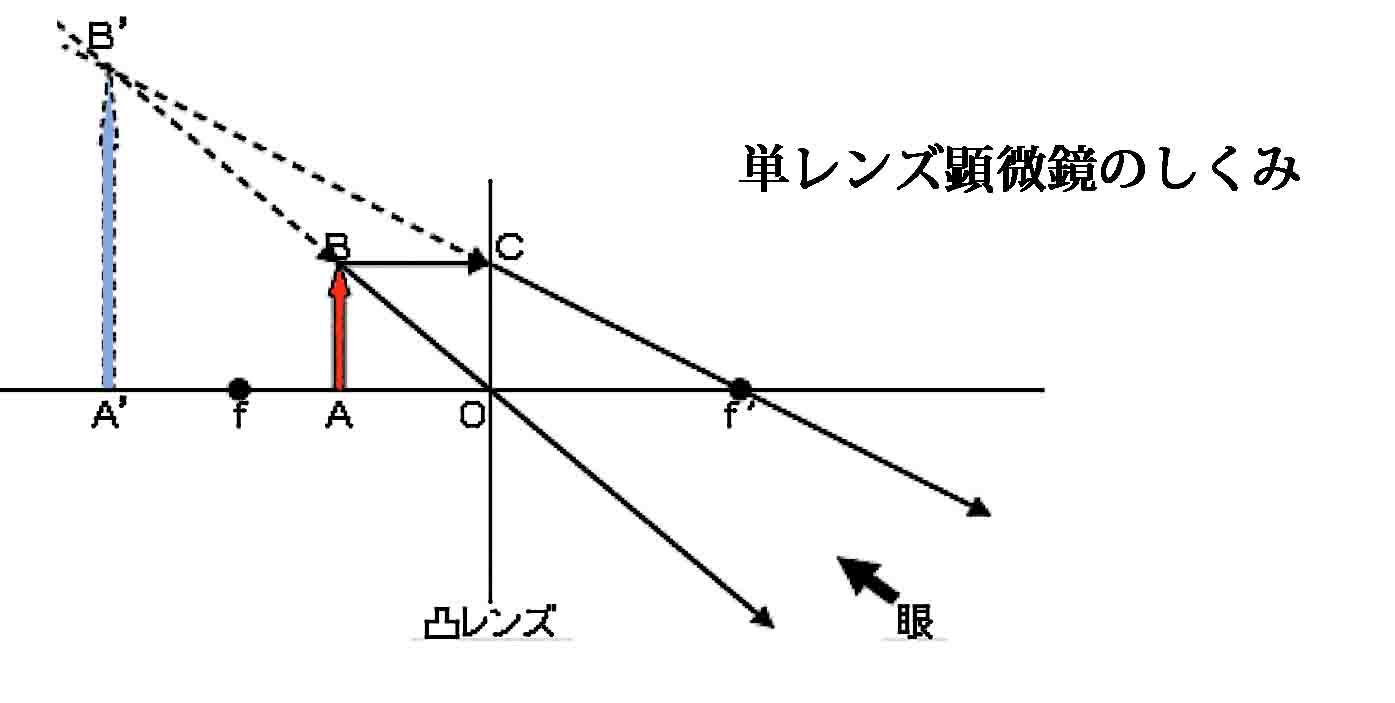
単レンズ顕微鏡の仕組み
単レンズ顕微鏡の仕組みを、書いてみました。レンズの焦点よりもレンズに近いところにおかれた物体(AB)の像は、A'B'のところに拡大されて作られます。
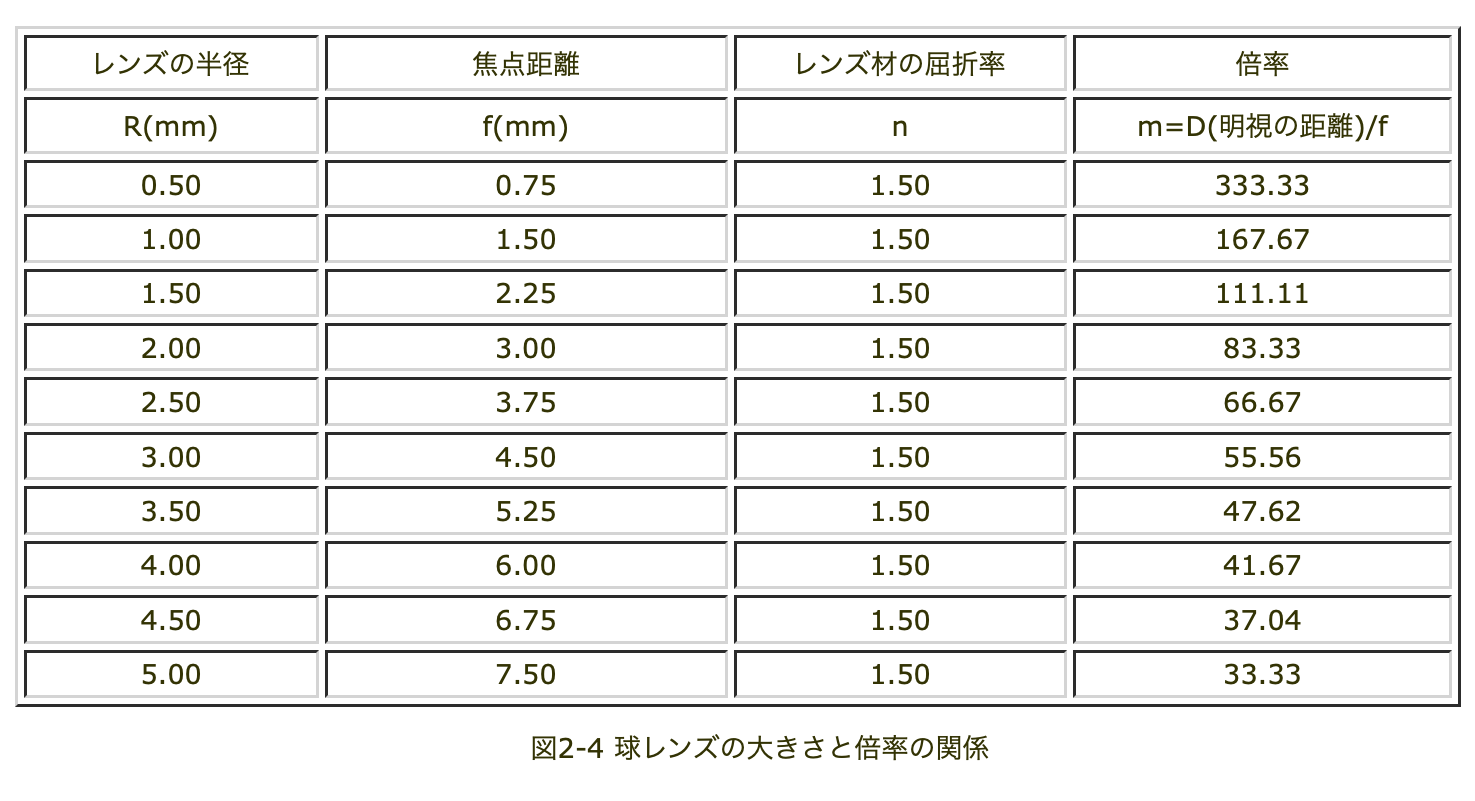
球レンズの大きさと倍率の関係
近似的にm=D/fで計算してあります。この表からも判るように、レンズの半径が小さいほど、拡大倍率が大きくなります。ただし、上のウィキペディアにも書いてあるように、収差などによって制限を受けます。レーベンフックの顕微鏡では、レンズに目を近づけ、観察しようとする試料を、レンズの反対側にかなり接近させなければならないことが判ります。
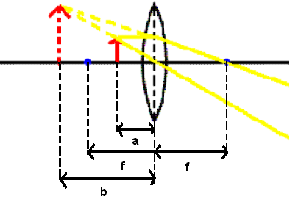
虫眼鏡のしくみ(フリー百科事典『ウィキペディア(Wikipedia)』より)
図1-2のような光学系を考える。前節で述べたように、凸レンズでは焦点よりもレンズ側に物体を置くと正立の虚像をつくる。このとき、(1-i) 式、(1-ii) 式を用いて倍率mをa、fであらわすと、
m=f/(a-f)‥‥(1-iii)
のようになる。この式から考えれば、焦点に近づけるほど倍率が上がるように思われる。しかし、レンズには分解能、収差というものがあり、拡大されていても人間の眼は視認できなくなってしまう。一般的に虫眼鏡に表示された倍率は明視の距離 (個人差はあるが一般的に250mmとされている) と呼ばれる人間が最も視認しやすい距離における虫眼鏡の拡大倍率が表示されている。
単レンズの大きさと倍率の関係を図2-4にまとめてみました。近似的にm=D/fで計算してあります。この表からも判るように、レンズの半径が小さいほど、拡大倍率が大きくなります。ただし、上のウィキペディアにも書いてあるように、収差などによって制限を受けます。レーベンフックの顕微鏡では、レンズに目を近づけ、観察しようとする試料を、レンズの反対側にかなり接近させなければならないことが判ります。
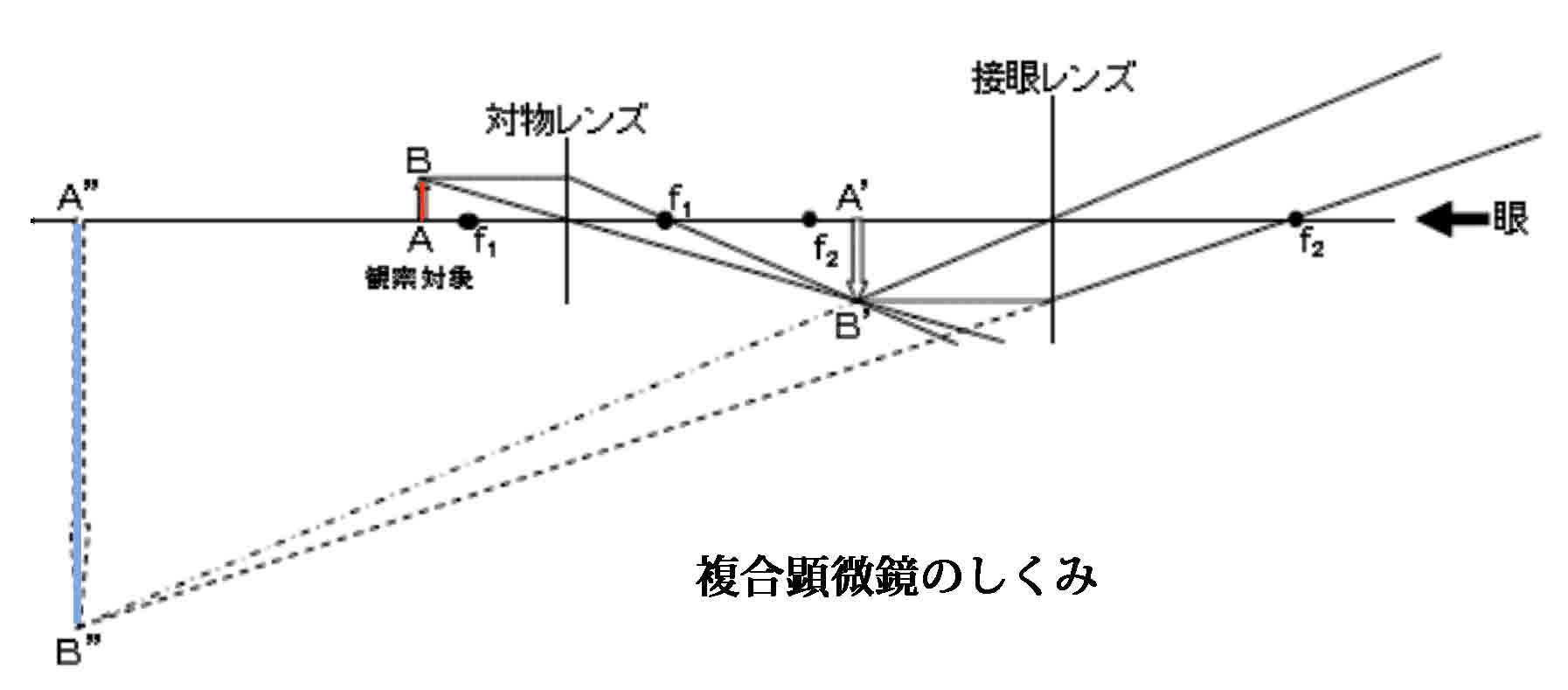
レンズを2枚以上用いた腹式顕微鏡は、ロバート・フックの時代以前にも使われていました。16世紀末にオランダのヤンセン親子(Hans & Zacharias Jansens)が発明したといわれています。基本的な原理は、1枚目のレンズ(対物レンズ)によって、焦点なの内側に実像(A'B')を作り、この像を、2枚目のレンズ(接眼レンズ)によって拡大して虚像(A''B'')を作り観察するということです。
シングルレンズ顕微鏡の作り方(その①)






シングルレンズ顕微鏡の作り方(その②)


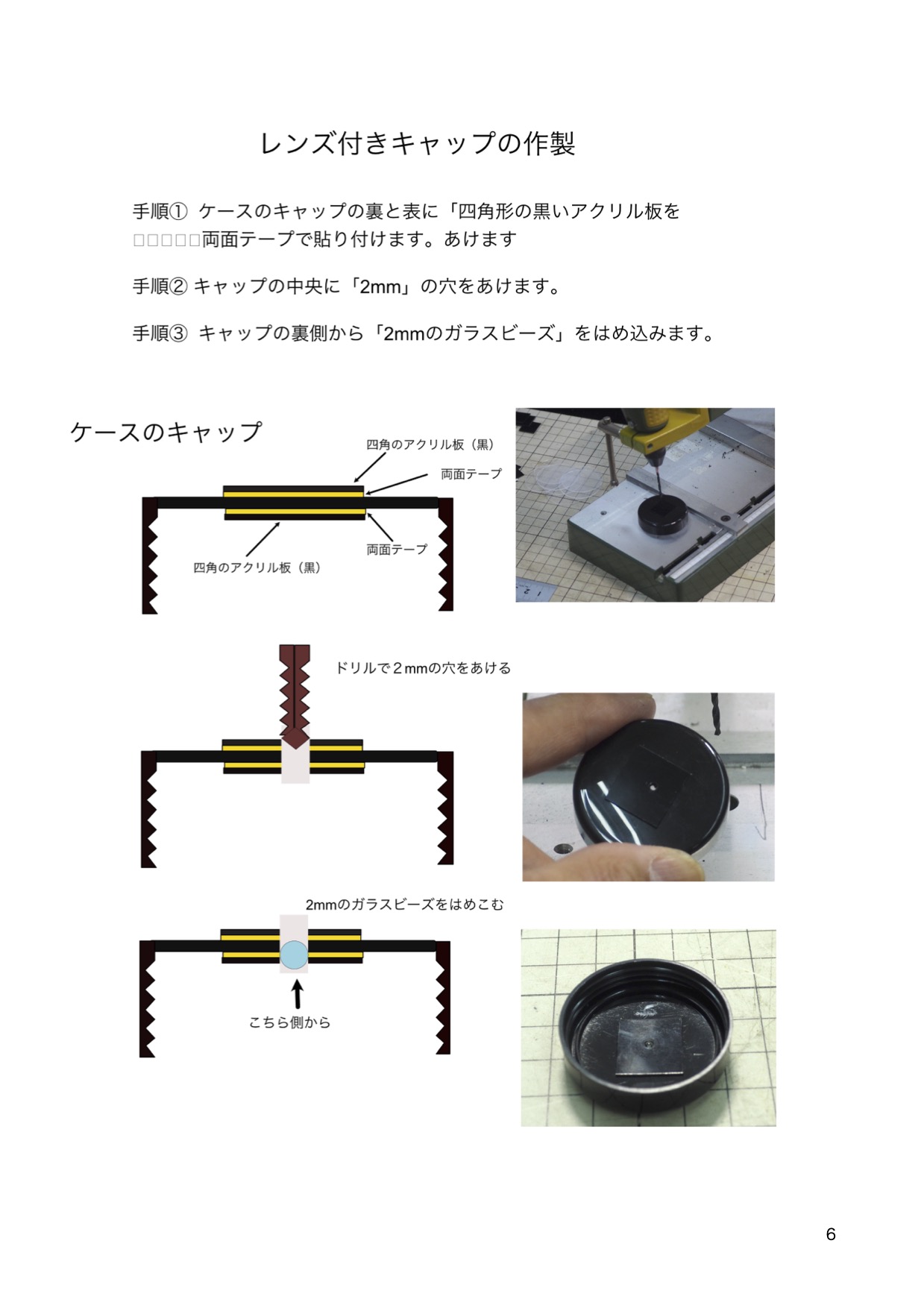


シングルレンズ顕微鏡の作り方(その③)



ペットボトル顕微鏡の作り方)







がんばって作ってみてください。
当初は、「ペットボトル」を使って、いわゆる「ペットボトル顕微鏡」を作っていましたが、子どもたちが、それだけのために「ペットボトル」飲料を購入するのも環境に良くないので、いろんな形の「シングルレンズ顕微鏡」を考えてみました。このページを参考にして、いりいろとトライしてみてください。

